This article is continuation of my article that you can find in below link.
Deep Learning- Understanding Receptive field in Computer Vision
In last article, we mentioned that convolutions are the key operations that enable Convolutional Neural Network (CNN) to extract features, create various channels and thereby increase receptive field (RF). In this article, we will check how convolutions performs these. Below is an animated image of 4×4 convolved by a 3×3 kernel to give 2×2 channel. Channels are the output of convolutions. Convolutions extract features and save it in channels. Channels are also called feature maps.
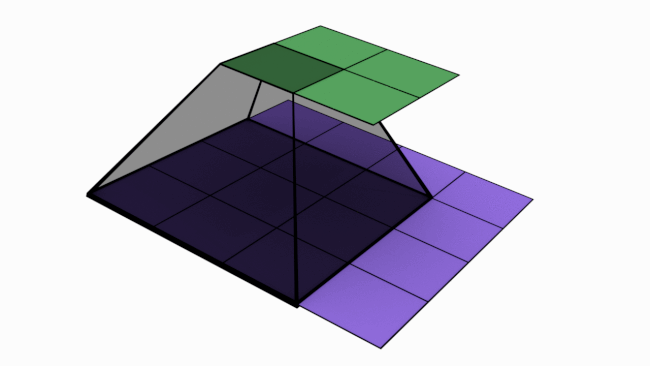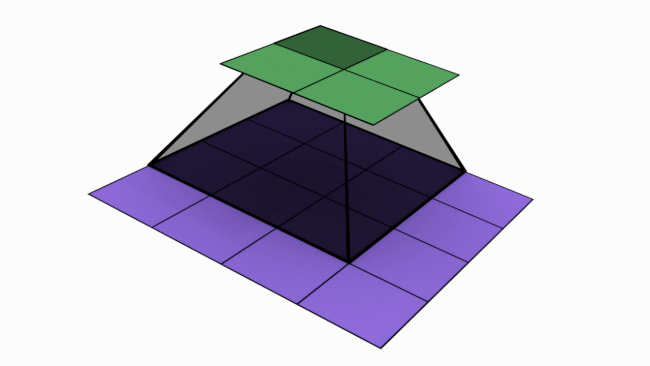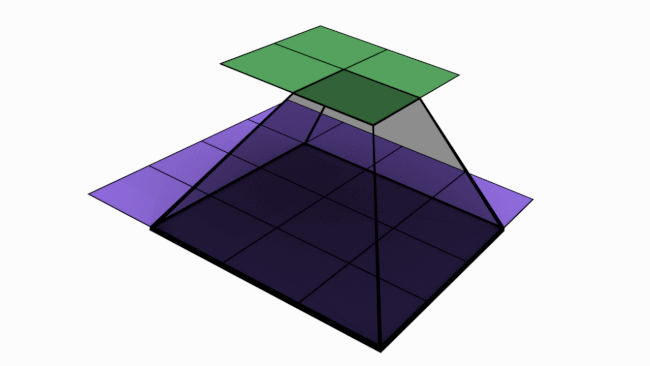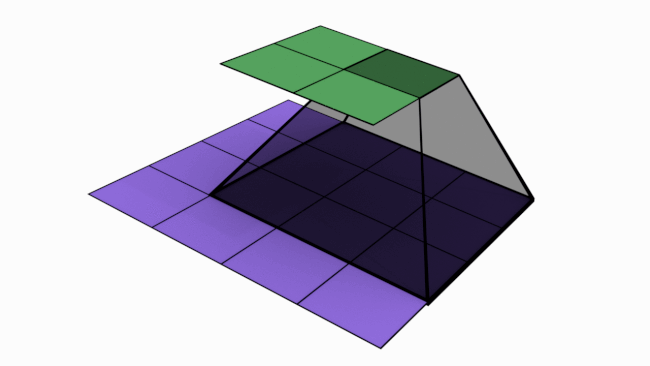
Let us look at an analogy to understand channels better. Imagine a musical band playing. We can hear song along with sound of musical instruments. All these in harmony only will make the performance worth listening. Now imagine the components of this musical play like human voice, guitar, drums etc. Each of these components when extracted and stored can be called as channels/feature maps.

How values are populated in channel cells via convolutions is as shown below. Below example is without padding.

Padding
In the first animation, if you noticed, all the pixels are not convolved same number of times. Only the central pixel is covered 9 times. Rest of the pixels are convolved lesser times. If we are not retaining the size, box will keep shrinking and central portion getting covered 9 times (when we use 3×3 kernel) also will shrink accordingly. If we are not convolving enough times CNN may not be able to extract all required features. Below is an image of padding = 1 applied on 6×6 image.
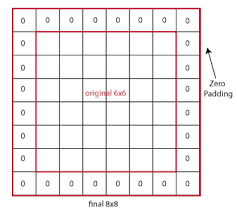
One of the advantages of using padding is that we can retain the central portion available for convolutions. Padding means adding additional columns and rows on borders. Though in above image we filled padded rows and columns with zeros, in general we fill them with border values. Please check the below image to understand how central portion increases as size increases.

However in previous article, we seen that retaining same size throughout is not viable. So how will we solve this problem – i.e. retaining the size vs reducing the size progressively ? We can achieve this by using blocks and layers as explained below.
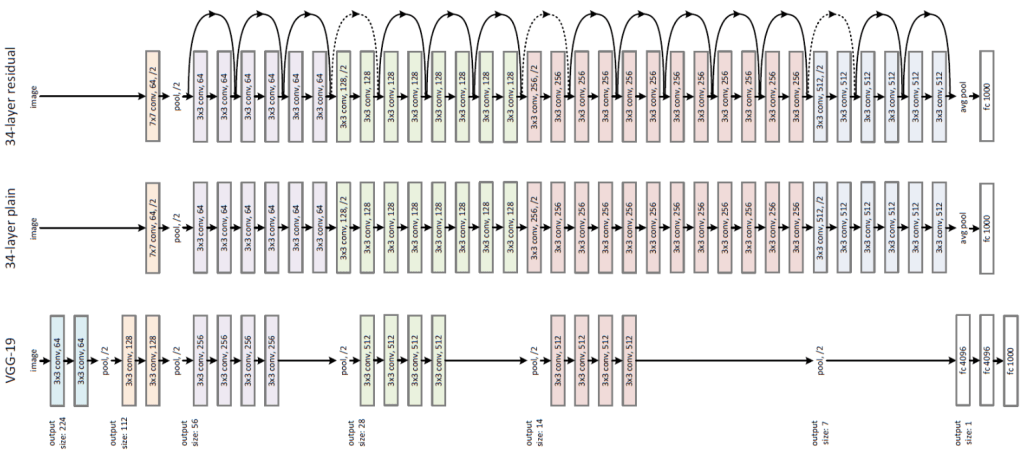
Please check the middle one in above diagram (34-layer plain). What you are seeing is a model architecture that has 4 blocks with 6 layers, 8 layers, 12 layers and 6 layers respectively. You can identify these blocks based on color change. Here, we are retaining same channel size per block using padding. At the end of each block we will down-size the channels using an operation called Maxpooling. Channel size reduction per block will happen something similar as below:
Block 1 -> 56×56
Block 2 -> 28×28
Block 3 -> 14×14
Block 4 -> 7×7
Disclaimer : There are other purposes also behind keeping block-layer architecture and using padding. But more on it later.
But how convolutions are extracting features ?
Let us understand this with a simple example. Feature extraction starts with basic edges/gradients and then these features are convolved to create more complex features like patterns, parts of objects and objects. Let us see how convolutions extract a vertical edge. Please note that higher numbers in below example represent brighter pixels i.e. 10 will be brighter than zero. An edge is detected when there is a sharp change in pixel values.
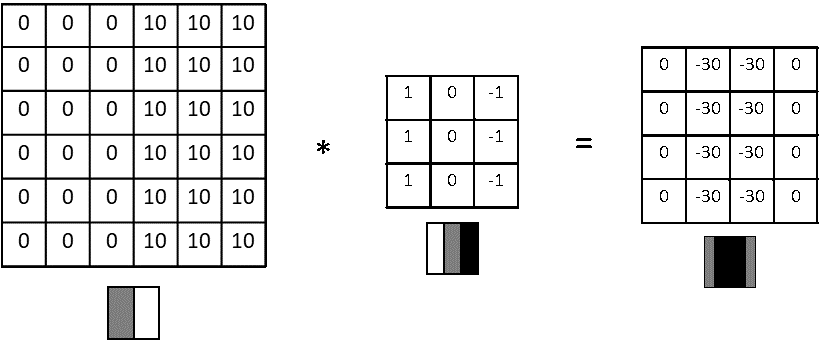
Here a 6×6 input is convolved with 3×3 kernel to give a 4×4 channel output. The values that you are seeing inside kernel are called weights. Now let us inspect what is happening from a physical sense.
6×6 input -> Imagine this as a portion of image where a vertical edge is there. Like the wall of a building where there is sudden transition from wall (dark pixels) to outside sunny world (bright pixels). You can see the values stacked up as 0s on left and 10s on right.
3×3 kernel -> Rather than seeing this as a kernel, imagine this as a feature extractor. In this case, our feature extractor is specialized in vertical edge extraction. How ? Please notice the weights inside this kernel. We have a bright left column (pixel values 1), then a dark middle column (pixel values 0) and finally a darker right column (pixel values -1). Basically kernel weights are build in such a way that it is transitioning from bright to dark to darker.
Output -> We have already seen how sum of products happen during convolution and how we arrive at output channel values. Interesting thing here is we extracted a vertical dark edge using above convolution. Check the image above. We got a 2 column width dark edge extracted and stored in a 4×4 channel (feature map). Follow-up question : How we got a much darker edge in output, when input edge was not this dark ? Answer : We increased the amplitude of dark edge we seen in input so that it won’t get diluted in future convolutions.
View more examples of edge extractors as below.
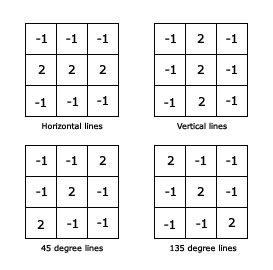
Below image will help you to visualize how edges play a role in an image.
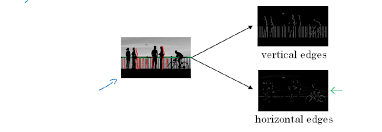
What are strides ?
Stride is the number of pixels that shift over when kernel convolves over input. Strides plays a role in determining output channel size as well as receptive field. In first image we seen stride of 1. Below is a convolution with a stride of 2.
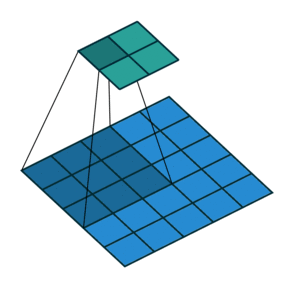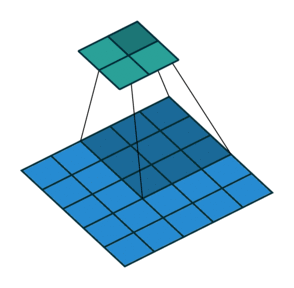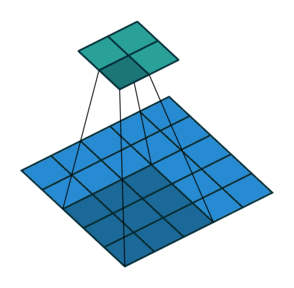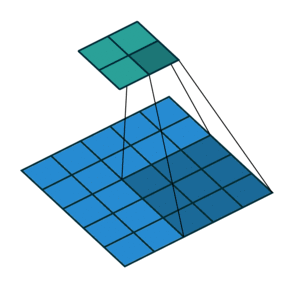
Since we now understand what is stride and padding, let us generalize the output size as below.

Convolution with multiple kernels to give multiple Channels
So far we have seen convolutions with one kernel to give one channel i.e. we were discussing in 2D like 7×7 * 3×3 -> 5×5. But in real networks, we create multiple channels layer-by layer or block-by-block. In below image you can see channels increasing in the order 1 – 25 -25 -32 -32 – 64.
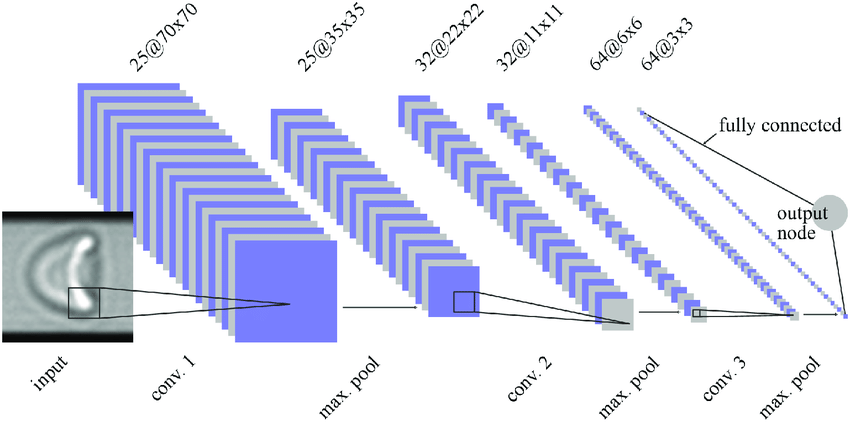
Let us inspect this in detail. We need to note below points while convolving with multiple kernels to get multiple channels.
– No: of channels in kernels need to be same as number of channels in input
– No: of kernels you want to convolve depends on number of channels you want in output.
For example:
28x28x3 * 3x3x3x32 -> 26x26x32
28x28x3 -> Imagine this as 28×28 dimensional matrices stacked one on top another 3 times. Rectangular prism with l, w =28 & depth = 3
Kernel size -> 3x3x3 Imagine this as 3×3 dimensional matrices one on top of another 3 times. Like a cube with all sides as 3.
Here no: of channels input (3) = no: of channels in kernel(3)
3x3x3x32 -> We are using 32 such types of 3x3x3 kernels
28x28x3 * 3x3x3x32 -> This means we are convolving 28x28x3 with 32 different types of 3x3x3
Result is 26x26x32 -> We will get 32 channels of 26×26 size
Here no: of kernels we used in convolution (32) = No: of channels in output (32)
Below is an animated representation multiple kernels convolving to give multiple channel outputs. Here input is 5x5x3. As input channel size is 3, we need to have 3 channels in kernel as well. We are using a 3×3 kernel here. So after considering the number of channels also, we can call it a 3x3x3 kernel. We are using 4 such kernels which makes it 3x3x3x4. We are convolving 5x5x3 with 3x3x3x4 to give us 3x3x4 outputs i.e. 4 channels of 3×3 size. (No padding used)
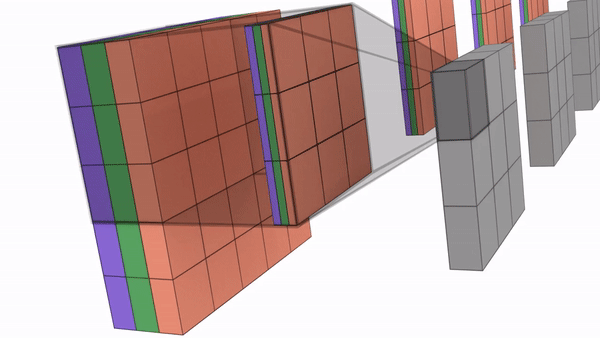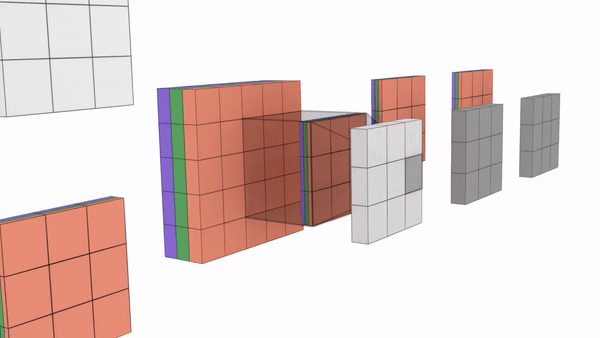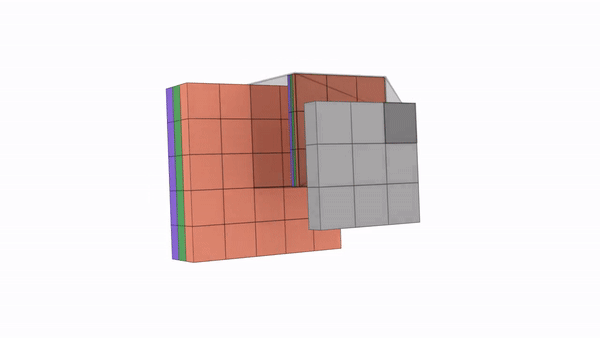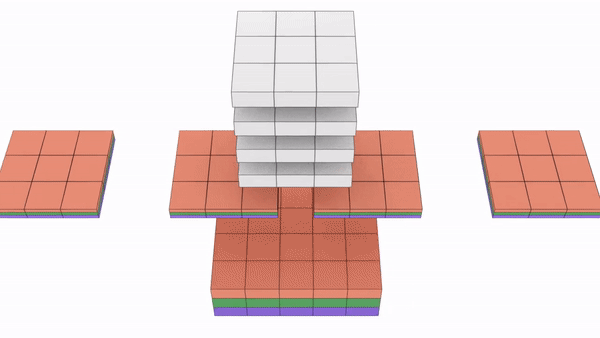
You can understand the calculations behind this by going through the image below. Here a 7x7x3 is convolved by 3x3x3x1 to give a 5x5x1 output.
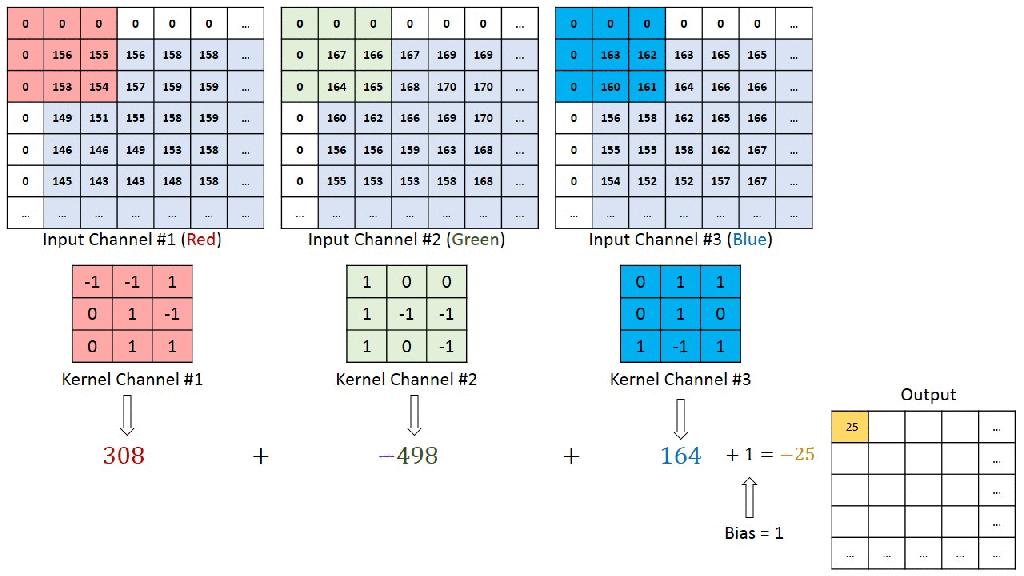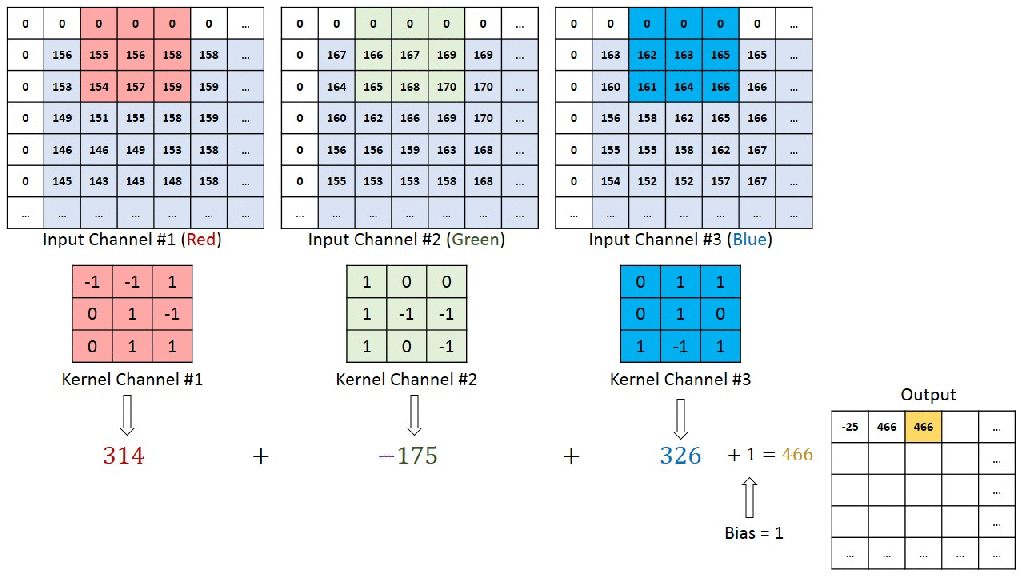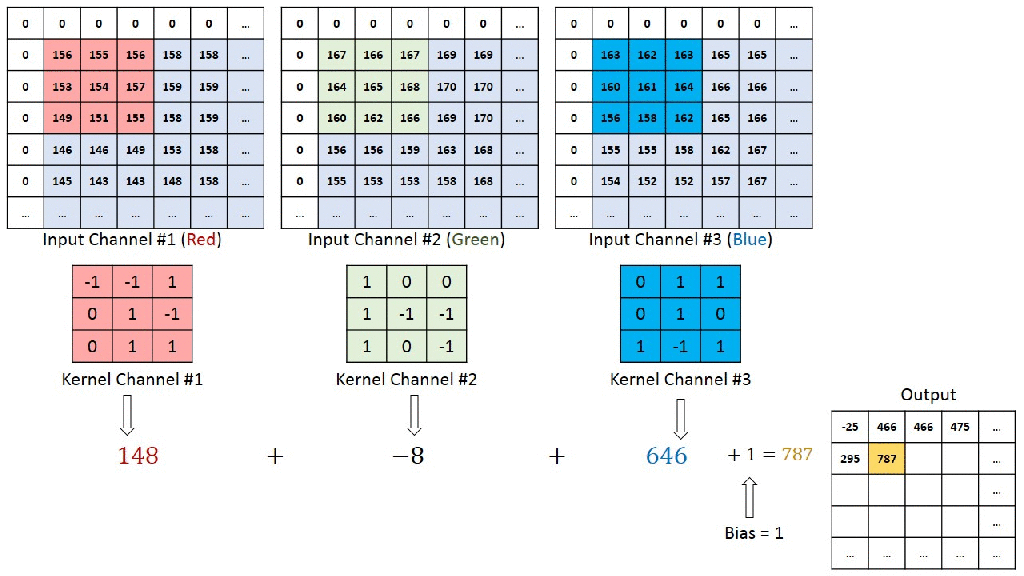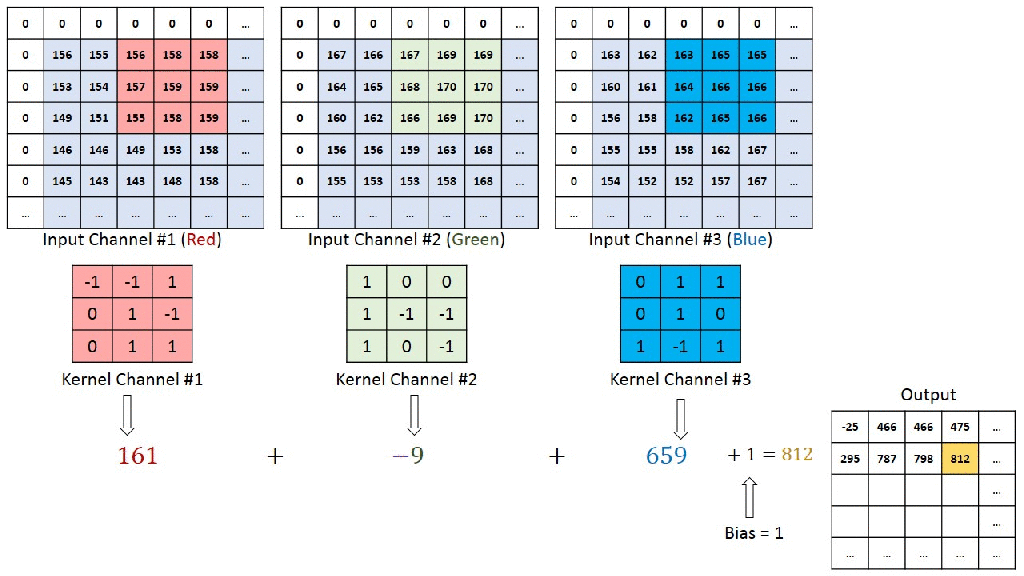
In next article, we will discuss about down sizing the channel size through maxpooling which is another type of convolution.